apply(arreglo, dimensión(es), función)18 FUNCIONES POR GRUPOS
El paquete base incluye una serie de funciones que permiten operar sobre subconjuntos de datos. Las más comunes son apply, sapply, lapply y tapply.
18.1 Función apply
La función apply se usa para aplicar una función sobre cada uno de los elementos dimensionales de un arreglo1.
Cuando su argumento es una matriz, la función apply aplica una función determinada a cada una de sus filas (dimensión 1) o columnas (dimensión 2).
El formato general es el siguiente:
El primer argumento de la función apply corresponde al nombre del arreglo. El segundo argumento se refiere al indicador numérico de la dimensión: 1 para las filas de una matriz (o primera dimensión de un arreglo), 2 para las columnas de una matriz (o segunda dimensión de un arreglo), 3 para la tercera dimensión de un arreglo y así sucesivamente. El tercer argumento de apply es el nombre de la función que se aplicará sobre los elementos dimensionales del arreglo.
Deben tenerse presentes los siguientes aspectos para la adecuada definición del argumento FUN (tercer argumento de apply):
El nombre de la función se escribe respetando sus particularidades, en cuanto a la diferenciación entre mayúsculas y minúsculas.
Aunque las ayudas de la función
applyindican que el nombre de la función que sirve de valor al argumentoFUNdebe escribirse entrecomillado (o con comillas invertidas), también puede escribirse sin comillas.Después del nombre no se escriben paréntesis.
Únicamente se escribe el nombre de la función. Si fuera necesario incluir argumentos para dicha función, estos irían en las posiciones sucesivas (cuarta y siguientes), separados por coma e introducidos mediante su nombre.
Considérese la matriz m2, conformada por 2 filas y 3 columnas.
[,1] [,2] [,3]
[1,] 2 0 5
[2,] -1 9 1Para obtener los promedios por fila de la matriz m2, indicando que deben retirarse los valores perdidos, en caso de que los hubiese, se usa la siguiente instrucción:
apply(m2, 1, mean, na.rm = T)[1] 2.333333 3.000000El resultado es un vector con dos elementos: el promedio de la primera fila y el promedio de la segunda fila.
¿Cómo se obtendría la suma de los elementos en cada una de las columnas? ¿Cuántos elementos tendrá el vector resultante?
Debido a la naturaleza de las funciones usadas en los dos ejemplos anteriores (media y suma) —que presentan un ‘resumen’ de cada uno de los elementos dimensionales— el resultado ha sido un vector. No obstante, cuando se aplica una función sobre cada uno de los elementos del arreglo, el resultado es otro arreglo.
Consideremos nuevamente la matriz m2:
[,1] [,2] [,3]
[1,] 2 0 5
[2,] -1 9 1Supóngase que se quiere obtener el rango de los elementos dentro de cada una de sus filas:
apply(m2, 1, "rank") [,1] [,2]
[1,] 2 1
[2,] 1 3
[3,] 3 2Este resultado puede no ser fácilmente visualizable, por la manera en la que se organiza: la consulta sobre los rangos de los elementos de la primera fila de m2 genera un vector; la consulta sobre los rangos de los elementos de la segunda fila de m2 genera un segundo vector. Estos dos vectores se organizan por columnas en la matriz resultante.
Para tener una visualización más directa del resultado, basta con trasponer la matriz resultante, así:
t(apply(m2, 1, rank)) [,1] [,2] [,3]
[1,] 2 1 3
[2,] 1 3 2Esta trasposición facilita conectar visualmente los valores de la matriz de rangos con los de la matriz de origen. Puede observarse, por ejemplo, la siguiente asignación de rangos para los elementos de la primera fila de m2:
Rango 1 para el valor 0, rango 2 para el valor 2 y rango 3 para el valor 5.
Cuando se aplica alguna función a cada uno de los elementos dimensionales de un arreglo y el resultado de cada uno de tales elementos es un vector, los diferentes vectores se organizan por columnas, sin importar si la función se aplica por filas o por columnas.
Consecuentemente, cuando la función se aplique por columnas, el resultado se visualizará directamente, sin trasposición.
Considérese nuevamente la matriz m2:
[,1] [,2] [,3]
[1,] 2 0 5
[2,] -1 9 1Ahora, considérese la aplicación de rangos por columnas:
apply(m2, 2, rank) [,1] [,2] [,3]
[1,] 2 1 2
[2,] 1 2 1Definamos ahora un arreglo tetradimensional, con 5 elementos en la primera dimensión, 4 elementos en la segunda, 2 elementos en la tercera y 3 elementos en la cuarta.
arreglo <- array(1:120, c(5, 4, 2, 3))Para facilitar la conceptualización de este arreglo tetradimensional, podríamos imaginarlo como una serie de tres cubos, cada uno de los cuales tiene 5 filas, 4 columnas y dos elementos de profundidad, tal y como se ilustra en la figura 18.1.
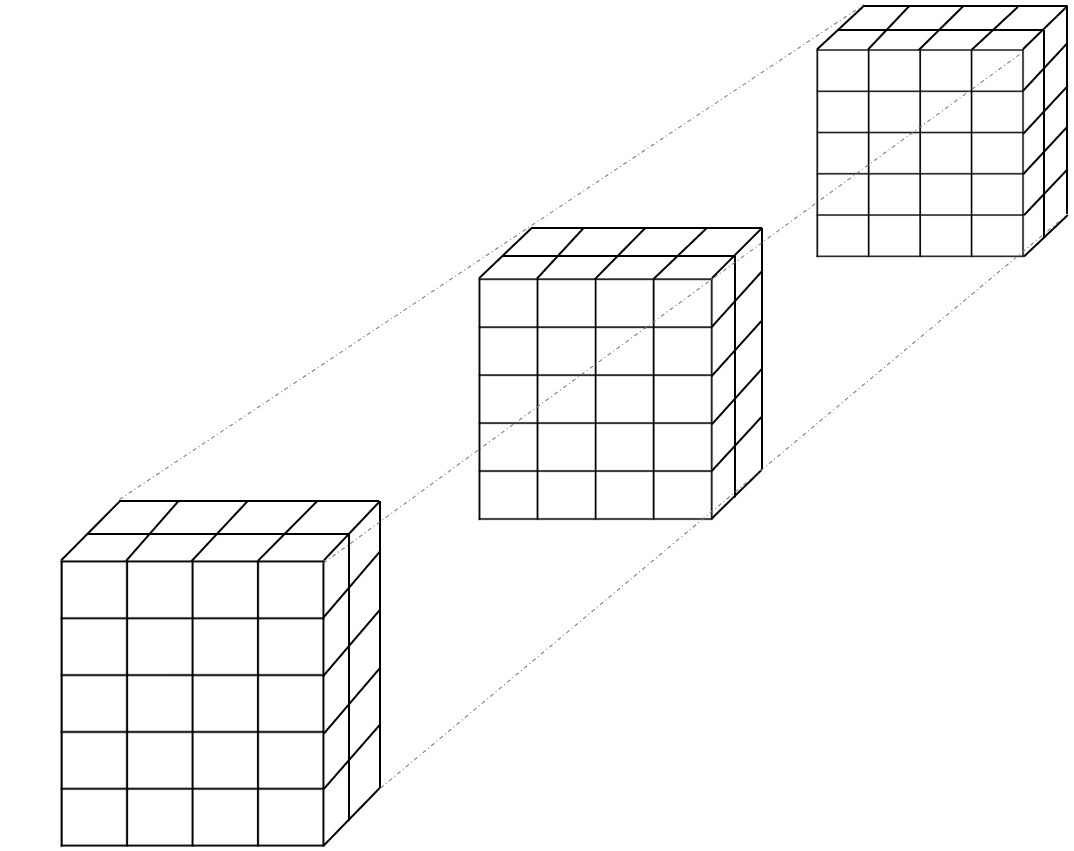
Para obtener los promedios de la cuarta dimensión, se usa la siguiente instrucción:
apply(arreglo, 4, mean)[1] 20.5 60.5 100.5Puesto que la cuarta dimensión está conformada por 3 elementos dimensionales2, se obtienen 3 promedios. Tomando la figura 18.1 como guía, serían los promedios de los cubos. Es decir que para cada cubo se están promediando todos los valores de las filas, las columnas y la profundidad.
La función apply también permite consolidar información de dos o más dimensiones.
Así, podrían obtenerse, por ejemplo, las medias podadas de las dimensiones 1 y 3 de arreglo, lo que equivaldría a promediar sobre las dimensiones 2 y 4. Tomando como guía la figura 18.1 sería el promedio de una fila particular en una cara particular. Para cada una de las combinaciones fila x cara (10 en total), se estarían promediando las diferentes columnas (dimensión 2) y los diferentes cubos (dimensión 4).
apply(arreglo, c(1, 3), mean, trim = 0.1) [,1] [,2]
[1,] 48.5 68.5
[2,] 49.5 69.5
[3,] 50.5 70.5
[4,] 51.5 71.5
[5,] 52.5 72.5El resultado es una matriz de 5 filas (número de elementos dimensionales de la dimensión 1 de arreglo) y 2 columnas (número de elementos dimensionales de la dimensión 3 de arreglo).
Así, por ejemplo, el elemento [3, 2] de la matriz resultante (70.5) corresponde a la media podada al 10 % de la fila 3, cara 2 de las 4 columnas y los 3 cubos (cf. figura 18.1).
Si bien es cierto que los arreglos de dimensión mayor que 2 no son los objetos más populares en R y que la mayoría de necesidades suelen resolverse con objetos más sencillos, bien podrían ser de utilidad en algunas aplicaciones específicas como la que se ilustra en el tip 8.1.
Aunque la función apply está diseñada para trabajar sobre arreglos, también admite data frames, en cuyo caso se coercionan implícitamente a matrices3 antes de generar el resultado.
Para ilustrarlo, generemos un data frame con la misma información de m2:
df <- data.frame(v1 = c(4, 8, 5, 6),
v2 = c(0.1, 0.8, 0.9, 1.1),
v3 = c(23, 89, 145, 213))
df v1 v2 v3
1 4 0.1 23
2 8 0.8 89
3 5 0.9 145
4 6 1.1 213La desviación estándar de cada una de las variables de df se obtiene así:
apply(df, 2, sd) v1 v2 v3
1.7078251 0.4349329 80.8682055 18.2 Funciones sapply y lapply
Las funciones sapply y lapply están diseñadas para operar sobre las columnas de un data frame o sobre los componentes de una lista4. La diferencia entre sapply y lapply está en la clase del objeto resultante.
El resultado de la función
sapplyse simplifica siempre que sea posible, generando vectores en la mayoría de los casos.El resultado de la función
lapplynunca se simplifica; siempre es una lista.
Consideremos nuevamente el data frame df:
v1 v2 v3
1 4 0.1 23
2 8 0.8 89
3 5 0.9 145
4 6 1.1 213Calculemos la desviación estándar de cada variable, usando la función sapply:
sapply(df, sd) v1 v2 v3
1.7078251 0.4349329 80.8682055 Puesto que cada uno de los 3 resultados (la desviación estándar de la primera columna, la desviación estándar de la segunda columna y la desviación estándar de la tercera columna) es un vector de longitud 1, el resultado puede simplificarse combinándolo en un vector.
Usemos ahora la función lapply para obtener la desviación estándar de cada variable:
lapply(df, sd)$v1
[1] 1.707825
$v2
[1] 0.4349329
$v3
[1] 80.86821Aunque se obtienen los mismos valores que con la función sapply, estos no se presentan de forma simplificada en un vector, sino que se mantienen en una lista compuesta por 3 vectores de longitud 1.
sapply y lapply para evaluar las columnas de un data frame!
En el contexto de análisis de datos, la obtención de información a partir de las columnas de un data frame es una práctica habitual.
Como se habrá notado, los resultados obtenidos anteriormente coinciden (excepto por el formato) con los que se obtienen al usar la función apply con el argumento MARGIN = 2 (cf. sección 18.1). En tal sentido, cualquiera de las anteriores opciones es igualmente válida, siempre que se especifiquen adecuadamente los argumentos.
No obstante, sapply o lapply constituyen alternativas más seguras y expresivas, por las siguientes razones:
Operan directamente sobre las columnas, sin necesidad de especificar
MARGIN. Esto, además de hacer la escritura más fluida, evita los errores que surgirían por la posible especificación incorrecta de este argumento.Respetan las clases originales de las columnas (no las convierten en una matriz).
Facilitan la lectura del código.
Por estas razones, se recomienda utilizar sapply o lapply cuando se trabaja con columnas de data frames, especialmente en contextos de análisis de datos.
NA
Al usar las funciones sapply o tapply con funciones como mean, median, sum, var y sd también puede agregar el argumento na.rm = T para omitir las NA antes de realizar la operación.
Considérese la aplicación de la función median, con el valor por defecto para el retiro de valores faltantes: na.rm = FALSE:
df <- data.frame(v1 = 1:5, v2 = 6:10, v3 = c(11:14, NA))
sapply(df, median)v1 v2 v3
3 8 NA Considérese ahora la misma función, removiendo las NA:
sapply(df, median, na.rm = T) v1 v2 v3
3.0 8.0 12.5 18.3 Función tapply
La función tapply permite aplicar una función sobre subconjuntos de elementos dentro de un arreglo, definidos con base en los niveles de uno o más factores.
Considérese el siguiente data frame, conformado por dos factores (f1 y f2) y por un vector numérico, y.
set.seed(12)
df <- data.frame(f1 = rep(c("a", "b", "c"), 12),
f2 = rep(c("A", "B", "C", "D"), each = 9),
y = rnorm(36))La siguiente instrucción genera los promedios de y, para cada uno de los niveles del factor f1.
medias.f1 <- tapply(df$y, df$f1, mean)
medias.f1 a b c
-0.2122834 0.1392543 -0.2819433 Análogamente, pueden obtenerse los promedios de y, para cada uno de los niveles de f2, así:
medias.f2 <- tapply(df$y, df$f2, mean)
medias.f2 A B C D
-0.5666838 -0.1930768 0.1846989 0.1017650 Asimismo, pueden obtenerse los promedios para cada una de las combinaciones de los niveles de f1 con los niveles de f2, especificando el segundo argumento como una lista, así:
medias.f1f2 <- with(df, tapply(y, list(f1, f2), mean))
medias.f1f2 A B C D
a -0.9053072 -0.3516720 0.49630826 -0.0884628
b -0.3495760 0.1410371 0.15042971 0.6151263
c -0.4451681 -0.3685954 -0.09264116 -0.2213684El objeto resultante de aplicar la función tapply tiene tantas dimensiones como factores se especifiquen en su segundo argumento.
El orden de las dimensiones corresponde con el orden en el que se hayan especificado los factores. Así, en el ejemplo anterior, las medias por niveles de f1 se organizan en filas, y las correspondientes a los niveles de f2 en columnas.
Las filas y las columnas de la matriz resultante se nombran automáticamente con los niveles de los factores usados para agrupar.
Este formato es útil para representar tablas cruzadas o resúmenes por combinación de niveles, pero puede requerir conversión adicional (por ejemplo, a un data frame) si se desea integrar el resultado en flujos de análisis posteriores.
Debe tenerse en cuenta que si alguna combinación de niveles no está presente en los datos, el resultado correspondiente será un valor NA, lo cual podría pasar desapercibido y afectar análisis posteriores.
na.rm = TRUE?
Al usar la función tapply con funciones como mean, median, sum, var y sd, también puede agregarse el argumento na.rm = T para omitir los valores NA antes de realizar la operación (cf. tip 18.1).
Esto no evitaría, sin embargo, la aparición de los NA señalados al final de la nota 18.1. En este último caso, los NA se deben a la inexistencia de una combinación particular de niveles de los factores; no a la presencia de observaciones faltantes dentro de un grupo existente.
En su acepción genérica, que también incluye matrices.↩︎
Algo equivalente a 3 filas o 3 columnas, pero no tienen un nombre particular.↩︎
Se les redefine su clase (cf. sección 10.7).↩︎
Estas funciones aplican sobre listas en términos genéricos, es decir, listas o data frames, acorde con lo ilustrado en las secciones 9.1 y 10.6.↩︎